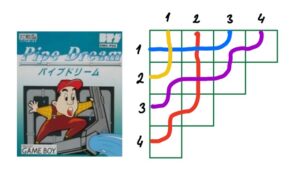
This Friday at 11am we welcome (on Zoom) Evgeny Smirnov from HSE in Moscow and Independent University of Moscow, he will talk about Schubert Polynomials for classical groups.

Here is his summary and his super image:

The varieties of flags have been studied since the 19th century; they appeared in the works of G.Graßmann and H.Schubert, who used them to answer questions of enumerative geometry. They have a remarkable cellular decomposition, called Schubert. The adhesion classes of these cells (Schubert classes) determine a distinguished basis in the cohomology ring. According to a classic result of A.Borel, they can be considered as elements of the quotient of the ring of polynomials in several variables; it is then interesting to find a presentation of Schubert classes by polynomials.

In 1982, A.Lascoux and M.-P.Schützenberger found such a presentation, canonical in a certain sense, by Schubert’s polynomials. These polynomials have a very rich and interesting combinatorial structure. They are obtained as the generating functions of certain strand diagrams, say pipe dreams; in particular, this implies the positivity of their coefficients.

We can consider the same constructions for the G/B flag varieties of other classic groups: SO(n) and Sp(2n). In these cases, the Schubert polynomials were defined by S.Billey and M.Haiman in 1995. I will present a new construction of pipe dreams for these polynomials, which appeared in our joint work with Anna Tutubalina.

1) At 9.30 am-10.30 am Frédéric Palesi will give an introductory talk about the variety of characters of surface groups

Summary: A hyperbolic surface S is naturally associated a (conjugation class of) representation of the fundamental group of the surface in the group of isometries of the hyperbolic plane. This more generally motivates the study of the space of (conjugation classes of) representations in SL(2,C). We will see how this space is associated with the character variety and can be set by a finite number of trace functions. The natural action of the mapping class group on the variety of characters can then be studied in a more algebraic way, and we will illustrate the dynamics of this action on simple examples of surfaces.

2) Then at 11am-12pm Carlos Matheus will talk about the
Elliptical dynamics on certain varieties of relative characters

Resume: In this paper, we will discuss the dynamics of the action of a
hyperbolic element of SL(2,Z) on some levels of SU varietes(2)
and SU(3) characters of an epoint torus. It is a work in common
with G. Forni, W. Goldman and S. Lawton.

4PM

The speaker is Oleg Lepski (AMU). Here is his title and summary.

Title: Majorantes pour une collection de variables aléatoires et la théorie de l’adaptation

Abstract: The main purpose of this talk is to look from a unique perspective at certain phenomena arising in different areas of probability theory and mathematical statistics. In particular, we will try to understand what is common between conventional probabilistic results, such as iterated logarithm law for example and the problem in adaptive estimation called price to pay for adaptation. Why are there two different types of this price? It turned out that all these problems and many other problems can be reduced to looking for the majorante (upper function) for a given collection of positive random variables.

This Friday, March 25 at 11am we will have the pleasure to welcome Philipp Gohlke (https://www.math.uni-bielefeld.de/~pgohlke/) who will speak to us about
Schrödinger operators associated with dynamic systems

Here is summary :

Spectral properties of Schrödinger operators are relevant for the behavior of quantum mechanical systems in the presence of an external potential. In many interesting cases, the potential can be generated via a dynamical system.
There is a partial understanding and some general heuristics on how the spectrum of the Schrödinger operator depends on the type of dynamical systems.
We will discuss some of the known results and explore how they change if the potential is modified by a periodic background (joint work with D.Damanik and J.Fillman).

Speaker: Pablo PORTILLA (Lille)

The Marseilles Federative Colloquium of Mathematics is intended for all mathematicians of the Marseilles agglomeration. It takes the form of one-hour lectures taking place on certain Fridays at the FRUMAM, on the Saint-Charles campus of the University of Aix-Marseille. Moment of conviviality, it is followed by a pot allowing to pleasantly end the week.

Title: Functions L and self-propelled periods

Abstract: Self-propelled forms are generalizations of modular forms that play a central role in the Langlands program. More precisely, the global Langlands correspondence postulates the existence of still mysterious relations between these analytical objects and categories of arithmetic objects such as elliptical curves. A point of contact between these two worlds is the theory of L-functions and an advantage of this correspondence, when established, is that self-propelled L-functions are generally better understood than their arithmetic analogues (especially from the analytical point of view).
In the 1980s, Waldspurger discovered new and surprising relationships between the central value of certain self-propelled L functions and “toric periods” of self-propelled forms for GL(2). This Waldspurger formula had many applications (notably to the conjecture of Birch and Swinnerton-Dyer) and in the mid-2000s Gan-Gross-Prasad and then Ichino-Ikeda formulated higher-ranking generalizations for all classical groups (orthogonal, unitary and symplectic). These conjectures again link central values of functions L to “self-propelled periods” that is, explicit integrals of self-propelled forms. They are now essentially established for unit groups. In this talk I will propose an introduction to this circle of ideas and I will give a state of the art on the subject.

This Friday, February 25 at 11am at the FRUMAM we will have the third session of the Rauzy seminar with the talk of Julien Boulanger around the points of connection on the translation surfaces.
there will also be the inauguration (in the presence of the artist! ) of the three works of Sylvie Pic that will now live at the FRUMAM! 🙂

Here is Julien’s summary (and attached images):

Title: Connection points on translation surfaces.
Abstract: After recalling the notions of translation surfaces and Veech group, we will focus on the notion of connection point, used in particular by P.Hubert and T.Schmidt to build translation surfaces of which the Veech group is infinitely generated. However, if we know how to characterize the connection points for type 2 translation surfaces and their coatings, we know almost nothing in the general case. In this talk we will focus on the particular case of the surface of the double heptagone, type 3, and in particular show that the central points of the double heptagone are not connection points, which answers in the negative to a question of P.Hubert and T.Schmidt.

And then, here you can discover some works by Sylvie Pic: http://www.documentsdartistes.org/artistes/pic/repro.html

Speaker: Raul OSET SINHA (Valencia)