Archives de catégorie : Séminaires et groupes de travail
Séminaire Rauzy – 15 Avril
Ce vendredi à 11h nous accueillons (sur Zoom) Evgeny Smirnov de HSE à Moscou et Université Indépendante de Moscou, il nous parlera des Polynômes de Schubert pour les groupes classiques.
Voici son résumé et sa super image :
Les variétés de drapeaux ont été étudiées depuis le 19e siècle ; elles sont apparues dans les travaux de G.Graßmann et H.Schubert, qui les ont utilisées pour répondre à des questions de géométrie énumérative. Elles possèdent une décomposition cellulaire remarquable, dite de Schubert. Les classes des adhérences de ces cellules (les classes de Schubert) déterminent une base distinguée dans l’anneau de cohomologie. Selon un résultat classique de A.Borel, on peut les considérer comme éléments du quotient de l’anneau des polynômes en plusieurs variables; il est alors intéressant de trouver une présentation des classes de Schubert par des polynômes.
En 1982, A.Lascoux et M.-P.Schützenberger ont trouvé une telle présentation, canonique dans une certain sens précis, par les polynômes de Schubert. Ces polynômes ont une structure combinatoire très riche et intéressante. Ils sont obtenus comme les fonctions génératrices de certains diagrammes de brins, dites les pipe dreams; en particulier, cela implique la positivité de leurs coefficients.
On peut considérer les mêmes constructions pour les variétés de drapeaux G/B d’autres groupes classiques : SO(n) et Sp(2n). Dans ces cas-là, les polynômes de Schubert ont été définis par S.Billey et M.Haiman en 1995. Je vais présenter une nouvelle construction de pipe dreams pour ces polynômes, qui est apparue dans notre travail en commun avec Anna Tutubalina.
Les variétés de drapeaux ont été étudiées depuis le 19e siècle ; elles sont apparues dans les travaux de G.Graßmann et H.Schubert, qui les ont utilisées pour répondre à des questions de géométrie énumérative. Elles possèdent une décomposition cellulaire remarquable, dite de Schubert. Les classes des adhérences de ces cellules (les classes de Schubert) déterminent une base distinguée dans l’anneau de cohomologie. Selon un résultat classique de A.Borel, on peut les considérer comme éléments du quotient de l’anneau des polynômes en plusieurs variables; il est alors intéressant de trouver une présentation des classes de Schubert par des polynômes.
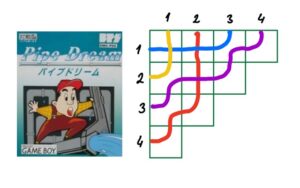
En 1982, A.Lascoux et M.-P.Schützenberger ont trouvé une telle présentation, canonique dans une certain sens précis, par les polynômes de Schubert. Ces polynômes ont une structure combinatoire très riche et intéressante. Ils sont obtenus comme les fonctions génératrices de certains diagrammes de brins, dites les pipe dreams; en particulier, cela implique la positivité de leurs coefficients.
On peut considérer les mêmes constructions pour les variétés de drapeaux G/B d’autres groupes classiques : SO(n) et Sp(2n). Dans ces cas-là, les polynômes de Schubert ont été définis par S.Billey et M.Haiman en 1995. Je vais présenter une nouvelle construction de pipe dreams pour ces polynômes, qui est apparue dans notre travail en commun avec Anna Tutubalina.
Séminaire Rauzy – 1er Avril
1) À 9h30-10h30 Frédéric Palesi donnera un exposé introductif concernant la variété de caractères de groupes de surfaces
Résumé : A toute surface hyperbolique S est naturellement associée une (classe de conjugaison de) représentation du groupe fondamental de la surface dans le groupe des isométries du plan hyperbolique. Cela motive de façon plus générale l’étude de l’espace des (classes de conjugaisons de) représentations dans SL(2,C). Nous verrons comment cet espace est associé à la variété des caractères et peut être paramétré par un nombre fini de fonctions trace. L’action naturelle du mapping class group sur la variété de caractères peut alors être étudiée de façon plus algébrique, et nous illustrerons la dynamique de cette action sur des exemples simples de surfaces.
2) Puis, à 11h-12h Carlos Matheus nous parlera de la
Dynamique elliptique sur certaines varietes de caracteres relatives
Resume: Dans cet expose, on discutera la dynamique de l’action d’un
element hyperbolique de SL(2,Z) sur certains niveaux des varietes de SU(2)
et SU(3) caracteres d’un tore epointe. Il s’agit d’un travail en commun
avec G. Forni, W. Goldman et S. Lawton.
Colloquium – 1er Avril
16H 00
L’orateur est Oleg Lepski (AMU). Voici son titre et son résumé.
Titre : Les majorantes pour une collection de variables aléatoires et la théorie de l’adaptation
Résumé : L’objectif principal de cette exposé est de regarder d’un point de vue unique à certains phénomènes découlant dans différents domaines de la théorie des probabilités et des statistiques mathématiques. En particulier, nous allons essayer de comprendre ce qui est commun entre les résultats probabilistes classiques, tels que la loi de logarithme itérée par exemple et le problème dans l’estimation adaptative appelée prix à payer pour l’adaptation. Pourquoi il existe deux types différents de ce prix? Il s’est avéré que tous ces problèmes et de nombreux autres problèmes peuvent être réduits à la recherche de la majorante (upper function) pour une collection donnée de variables aléatoires positives.
Séminaire Rauzy – 25 Mars
Ce vendredi 25 mars à 11h nous aurons le plaisir d’accueillir Philipp Gohlke (https://www.math.uni-bielefeld.de/~pgohlke/) qui nous parlera des
Opérateurs de Schrödinger associés aux systèmes dynamiques
Voici son résumé :
Spectral properties of Schrödinger operators are relevant for the behavior of quantum mechanical systems in the presence of an external potential. In many interesting cases, the potential can be generated via a dynamical system.
There is a partial understanding and some general heuristics on how the spectrum of the Schrödinger operator depends on the type of dynamical systems.
We will discuss some of the known results and explore how they change if the potential is modified by a periodic background (joint work with D.Damanik and J.Fillman).
Séminaire singularité – 17 Mars
Speaker: Pablo PORTILLA (Lille)
Title: Characterizing the geometric monodromy group of an isolated plane curve singularity
The abstract, as well as the list of the forthcoming speakers, is available on the website of the webinar: https://sites.google.com/view/singularites-marseille
The next talk will be in English, as well as future talks, in order to accommodate a larger public.
Colloquium – 11 Mars
Vendredi 11 Mars 16 H : intervenant : Raphael Beuzart-Plessis
Titre: Fonctions L et périodes automorphes
Résumé: Les formes automorphes sont des généralisations des formes modulaires qui jouent un rôle central dans le programme de Langlands. Plus précisément, la correspondance de Langlands globale postule l’existence de relations encore mystérieuses entre ces objets de nature analytique et des catégories d’objets arithmétiques tels que les courbes elliptiques. Un point de contact entre ces deux mondes est la théorie des fonctions L et un avantage de cette correspondance, lorsqu’elle est établie, est que les fonctions L automorphes sont en général mieux comprises que leurs analogues arithmétiques (notamment du point de vue analytique).
Dans les années 80, Waldspurger a découvert de nouvelles relations étonnantes entre la valeur centrale de certaines fonctions L automorphes et des “périodes toriques” de formes automorphes pour GL(2). Cette formule de Waldspurger a eu de nombreuses applications (notamment à la conjecture de Birch et Swinnerton-Dyer) et au milieu des années 2000, Gan-Gross-Prasad puis Ichino-Ikeda en ont formulé des généralisations en rang supérieur pour tous les groupes classiques (orthogonaux, unitaires et symplectiques). Ces conjectures relient à nouveau des valeurs centrales de fonctions L à des “périodes automorphes” c’est-à-dire des intégrales explicites de formes automorphes. Elles sont maintenant essentiellement établies pour les groupes unitaires. Dans cet exposé je proposerai une introduction à ce cercle d’idées et je donnerai un état de l’art sur le sujet.
Séminaire Rauzy – 11 Mars
Brocante mathématique
Séminaire RAUZY – Vendredi 25 février
Ce vendredi 25 février à 11h à la FRUMAM nous aurons la troisième séance du séminaire Rauzy avec l’exposé de Julien Boulanger autour des points de connexion sur les surfaces de translation.
il y aura aussi l’inauguration (en présence de l’artiste !) des trois œuvres de Sylvie Pic qui vont désormais vivre à la FRUMAM ! 🙂
Voici le résumé de Julien (et en pièce jointe ses images) :
Titre : Points de connexion sur les surfaces de translation.
Résumé : Après avoir rappelé les notions de surfaces de translation et de groupe de Veech, nous nous intéresserons à la notion de point de connexion, utilisée notamment par P.Hubert et T.Schmidt pour construire des surfaces de translation dont le groupe de Veech est infiniment engendré. Or, si on sait caractériser les points de connexion pour les surfaces de translation de genre 2 et leurs revêtements, on ne sait presque rien dans le cas général. Dans cet exposé on va s’intéresser au cas particulier de la surface du double heptagone, de genre 3, et notamment montrer que les points centraux du double heptagone ne sont pas des points de connexion, ce qui répond par la négative à une question de P.Hubert et T.Schmidt.
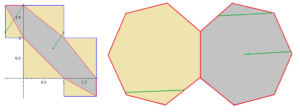
Et puis, ici vous pouvez découvrir quelques travaux de Sylvie Pic : http://www.documentsdartistes.org/artistes/pic/repro.html
Séminaire Singularité – Jeudi 24 février
The next session of the Marseille Singularity Webinar will take place Thursday, February 24th, from 14h00 to 15h00 (Paris time) via Zoom (see details below).
We will have the pleasure to listen to:
Speaker: Jean-Baptiste CAMPESATO (Angers)
Title: Motivic, logarithmic, and topological Milnor fibrations
The abstract, as well as the list of the forthcoming speakers, is available on the website of the webinar: https://sites.google.com/view/singularites-marseille
The next talk will be in English, as well as future talks, in order to accommodate a larger public.